CryptoHack教程的第三章：对称密码学。

Keyed Permutations

AES, like all good block ciphers, performs a “keyed permutation”. This means that it maps every possible input block to a unique output block, with a key determining which permutation to perform.

A “block” just refers to a fixed number of bits or bytes, which may represent any kind of data. AES processes a block and outputs another block. We’ll be specifically talking the variant of AES which works on 128 bit (16 byte) blocks and a 128 bit key, known as AES-128.

Using the same key, the permutation can be performed in reverse, mapping the output block back to the original input block. It is important that there is a one-to-one correspondence between input and output blocks, otherwise we wouldn’t be able to rely on the ciphertext to decrypt back to the same plaintext we started with.

What is the mathematical term for a one-to-one correspondence?

第一题是问一一对应在数学中的术语叫什么，我问了隔壁数学系的朋友才知道是双射。

答案是crypto{bijection}

Resisting Bruteforce

If a block cipher is secure, there should be no way for an attacker to distinguish the output of AES from a random permutation of bits. Furthermore, there should be no better way to undo the permutation than simply bruteforcing every possible key. That’s why academics consider a cipher theoretically “broken” if they can find an attack that takes fewer steps to perform than bruteforcing the key, even if that attack is practically infeasible.

How difficult is it to bruteforce a 128-bit keyspace? Somebody estimated that if you turned the power of the entire Bitcoin mining network against an AES-128 key, it would take over a hundred times the age of the universe to crack the key.

It turns out that there is an attack on AES that’s better than bruteforce, but only slightly – it lowers the security level of AES-128 down to 126.1 bits, and hasn’t been improved on for over 8 years. Given the large “security margin” provided by 128 bits, and the lack of improvements despite extensive study, it’s not considered a credible risk to the security of AES. But yes, in a very narrow sense, it “breaks” AES.

Finally, while quantum computers have the potential to completely break popular public-key cryptosystems like RSA via Shor’s algorithm, they are thought to only cut in half the security level of symmetric cryptosystems via Grover’s algorithm. This is one reason why people recommend using AES-256, despite it being less performant, as it would still provide a very adequate 128 bits of security in a quantum future.

What is the name for the best single-key attack against AES?

这一题也是单纯的讲解，答案就在上文蓝字的an attack中，即crypto{biclique}

Structure of AES

To achieve a keyed permutation that is infeasible to invert without the key, AES applies a large number of ad-hoc mixing operations on the input. This is in stark contrast to public-key cryptosystems like RSA, which are based on elegant individual mathematical problems. AES is much less elegant, but it’s very fast.

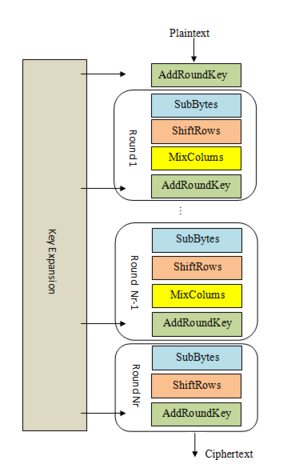
At a high level, AES-128 begins with a “key schedule” and then runs 10 rounds over a state. The starting state is just the plaintext block that we want to encrypt, represented as a 4x4 matrix of bytes. Over the course of the 10 rounds, the state is repeatedly modified by a number of invertible transformations.

Each transformation step has a defined purpose based on theoretical properties of secure ciphers established by Claude Shannon in the 1940s. We’ll look closer at each of these in the following challenges.

Here’s an overview of the phases of AES encryption:

1. KeyExpansion or Key Schedule

 From the 128 bit key, 11 separate 128 bit “round keys” are derived: one to be used in each AddRoundKey step.

1. Initial key addition

 AddRoundKey - the bytes of the first round key are XOR’d with the bytes of the state.

1. Round - this phase is looped 10 times, for 9 main rounds plus one “final round”

 a) SubBytes - each byte of the state is substituted for a different byte according to a lookup table (“S-box”).

 b) ShiftRows - the last three rows of the state matrix are transposed—shifted over a column or two or three.

 c) MixColumns - matrix multiplication is performed on the columns of the state, combining the four bytes in each column. This is skipped in the final round.

 d) AddRoundKey - the bytes of the current round key are XOR’d with the bytes of the state.

Included is a bytes2matrix function for converting our initial plaintext block into a state matrix. Write a matrix2bytes function to turn that matrix back into bytes, and submit the resulting plaintext as the flag.

Challenge files:
- matrix.py

Resources:
- YouTube: AES Rijndael Cipher explained as a Flash animation

这一节介绍了AES的结构，题目则是让我们写函数实现矩阵转换为bytes字符串。

def matrix2bytes(matrix):
    text=''
    for i in range(len(matrix)):
        for j in range(len(matrix[0])):
            text+=(chr(matrix[i][j]))
    return text

或者

def matrix2bytes(matrix):
    return bytes(sum(matrix, []))

答案为crypto{inmatrix}

Round Keys

We’re going to skip over the finer details of the KeyExpansion phase for now. The main point is that it takes in our 16 byte key and produces 11 4x4 matrices called “round keys” derived from our initial key. These round keys allow AES to get extra mileage out of the single key that we provided.

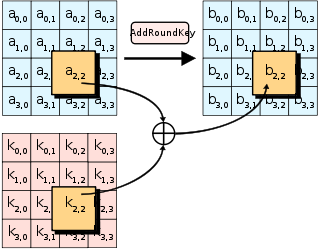
The initial key addition phase, which is next, has a single AddRoundKey step. The AddRoundKey step is straightforward: it XORs the current state with the current round key.

AddRoundKey also occurs as the final step of each round. AddRoundKey is what makes AES a “keyed permutation” rather than just a permutation. It’s the only part of AES where the key is mixed into the state, but is crucial for determining the permutation that occurs.

As you’ve seen in previous challenges, XOR is an easily invertible operation if you know the key, but tough to undo if you don’t. Now imagine trying to recover plaintext which has been XOR’d with 11 different keys, and heavily jumbled between each XOR operation with a series of substitution and transposition ciphers. That’s kinda what AES does! And we’ll see just how effective the jumbling is in the next few challenges.

Complete the add_round_key function, then use the matrix2bytes function to get your next flag.

Challenge files:
- add_round_key.py

这一节讲了AES中AddRoundKey这一操作，实际需要我们做的就是将两个矩阵中每一项分别异或并放入新矩阵。

def add_round_key(s, k):
    return [[sss ^ kkk for sss, kkk in zip(ss, kk)] for ss, kk in zip(s, k)]

得到

[[99, 114, 121, 112], [116, 111, 123, 114], [48, 117, 110, 100], [107, 51, 121, 125]]

再用上一题中的函数求得crypto{r0undk3y}